Introducing Qwen2-Math

Over the past year, significant research and development efforts have been focused on enhancing the reasoning capabilities of large language models, particularly in solving arithmetic and mathematical problems. Today, we are excited to unveil a new series of math-specific large language models, known as the Qwen2 series. This series includes Qwen2-Math and Qwen2-Math-Instruct models, available in varying sizes of 1.5B, 7B, and 72B parameters.

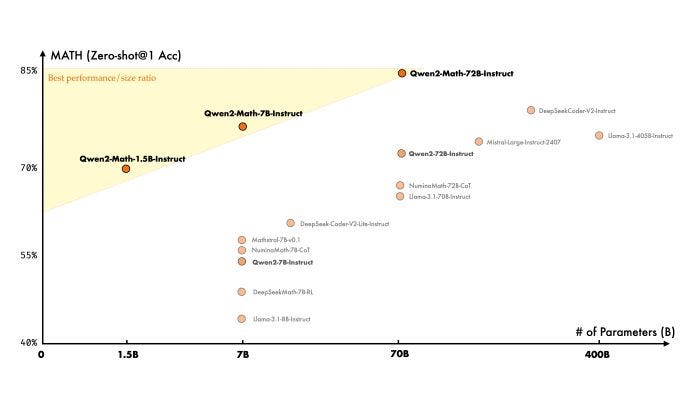
Qwen2-Math models are specialized to excel in mathematical tasks, outperforming both open-source models and leading closed-source models like GPT-4o. The goal of Qwen2-Math is to provide the community with powerful tools for tackling complex mathematical problems and advancing AI-driven mathematical research.

The performance of these math-specific models has been rigorously evaluated against various math benchmarks. Notably, the largest model in the series, Qwen2-Math-72B-Instruct, surpasses state-of-the-art models including GPT-4o, Claude-3.5-Sonnet, Gemini-1.5-Pro, and Llama-3.1–405B.

Qwen2-Math: Base Models

The Qwen2-Math base models are built on the foundation of the Qwen2–1.5B, 7B, and 72B models and are pretrained on a meticulously curated mathematics-specific corpus. This corpus includes a diverse range of high-quality mathematical content, such as web texts, books, codes, exam questions, and synthetic mathematical pre-training data generated by Qwen2.

These models were evaluated on three widely used English math benchmarks: GSM8K, Math, and MMLU-STEM. Additionally, they were tested on three Chinese math benchmarks: CMATH, GaoKao Math Cloze, and GaoKao Math QA. All evaluations were conducted using few-shot chain-of-thought prompting, a technique designed to assess the models’ reasoning and problem-solving capabilities in mathematics.

Qwen2-Math-Instruct: Instruction-Tuned Models

The Qwen2-Math-Instruct models take the base models a step further by incorporating instruction-tuning. This process begins with training a math-specific reward model based on Qwen2-Math-72B. This model combines a dense reward signal, reflecting the quality of answers, with a binary signal indicating whether the answer was correct. The combined signal is used to construct Supervised Fine-Tuning (SFT) data through Rejection Sampling and is further utilized in reinforcement learning with Group Relative Policy Optimization (GRPO) after SFT.

The Qwen2-Math-Instruct models were evaluated on a range of challenging mathematical benchmarks in both English and Chinese. These benchmarks include well-known tests like GSM8K and Math, as well as more difficult exams such as OlympiadBench, CollegeMath, GaoKao, AIME2024, and AMC2023. For Chinese benchmarks, evaluations were conducted on CMATH, Gaokao (Chinese college entrance exam 2024), and CN Middle School 24 (High School Entrance Exam 2024).

Performance was measured using greedy, Maj@8, and RM@8 metrics in a zero-shot setting for most benchmarks, with a 5-shot setting used for multiple-choice problems (like MMLU STEM, GaoKao, and CN Middle School 24). The Qwen2-Math-Instruct models demonstrated superior performance, particularly with RM@8 outperforming Maj@8 in the 1.5B and 7B models, highlighting the effectiveness of the math reward model.

Performance in Complex Mathematical Competitions

The Qwen2-Math-Instruct models have also been tested in complex mathematical competition evaluations, such as AIME 2024 and AMC 2023. These models were evaluated across various settings, including Greedy, Maj@64, RM@64, and RM@256, consistently performing well and showcasing their capability to handle challenging mathematical problems.

Case Study

The Qwen2-Math series has been put to the test with a variety of math problems from prestigious competitions like the International Mathematical Olympiad (IMO) and other global math contests. Here are some of the test cases:

• Problem from IMO Shortlist 2002

• Problem from IMO Shortlist 2022

• Problem from IMO 2022

• Problem from International Zhautykov Olympiad 2020

• Problem from Baltic Way 2023

• Problem from Lusophon Mathematical Olympiad 2023

• Problem from Balkan MO 2023

• Problem from Math Odyssey

• Problem from USAMO 2010

• Problem from JBMO Shortlist 2011

All solutions provided were generated by the Qwen2-Math-Instruct models without any human modification. While these models show promising results, it is important to note that the accuracy of the solutions is not guaranteed, and there may be errors in the claims or processes presented.

Decontamination

To ensure the integrity and reliability of the Qwen2-Math models, rigorous decontamination methods were applied to both the pretraining and post-training datasets.

• Pretraining Data Decontamination: This process targeted math datasets, including GSM8K and MATH, and removed samples with significant overlaps with the test sets. Exact match techniques were used to eliminate identical samples, and a 13-gram deduplication technique was applied to filter out samples where the longest common sequence ratio exceeded 0.6. This method effectively removed samples that could cause contamination, ensuring the training data was as unique and uncontaminated as possible.

• Post-Training Data Decontamination: Similar decontamination efforts were made for post-training data, removing contaminated samples that overlapped with datasets such as GSM8K, MATH, Aqua, SAT Math, OlympiadBench, College Math, AIME24, AMC23, and others. This thorough decontamination process was crucial in maintaining the quality and performance of the Qwen2-Math models.

Summary

The Qwen2-Math series represents a significant advancement in enhancing the mathematical capabilities of large language models. Built upon the Qwen2 foundation, the flagship model Qwen2-Math-72B-Instruct has demonstrated superior performance in math-related tasks, outperforming well-known proprietary models like GPT-4o and Claude 3.5.

Currently, Qwen2-Math models support only English, but there are plans to release bilingual models supporting both English and Chinese. Further down the line, multilingual models are also in development. The ongoing goal is to continue improving the models’ abilities to solve increasingly complex and challenging mathematical problems, pushing the boundaries of what AI can achieve in the field of mathematics.

If you want more updates related to AI, subscribe to our Newsletter